Laplace变换的定义、性质

一、定义：
1、傅立叶变换：当一个时间函数f(t) 既满足狄里赫利条件，又满足绝对可积条件时，其傅立叶变换成立。正、反变换分别为：
　　
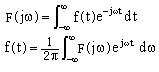
2、由傅立叶变换到Laplace变换：
　　在电气工程和无线电工程中，常见的函数一般均满足狄里赫利条件，但通常不满足绝对可积条件，因此不能直接进行傅立叶变换进行分析。函数不满足绝对可积条件的原因是当t→∞时，函数f(t)不衰减，或不但不衰减，反而增长。为了使f(t)变的绝对可积，选一个指数衰减因子即　　
　　在电路理论中，常常把换路的瞬间记为t=0，然后研究t＞0的过渡过程。这就是说，激励是从t=0开始作用于电路的，响应也应定义在t≥0。因此，傅立叶变换中积分的下限应定义为0-(考虑到由0-到0+可能发生跃变，故取0-)。即 　　　　　　　　　　　　　　　　　　　　　　　　　　
　　利用拉氏变换的定义计算下列各题。



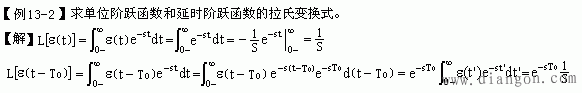
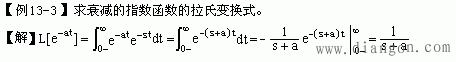
*对于常见函数的拉氏变换式可以记住，也可以查拉氏变换表。

二、拉氏变换的性质：（证明略）
　　利用拉氏变换的性质，可以简化函数的拉氏变换的计算。
性质1°：唯一性。象函数F(S)与半开区间 [0，∞)的时域函数f(t)存在一一对应的关系。
性质2°：线性性质。
　　设L[f1(t)]=F1(S)，L[f2(t)]=F2(S)
　　则：L[A1f1(t)±A2f2(t)]= A1F1(S)±A2F2(S)

性质3°：时域导数性质。
　

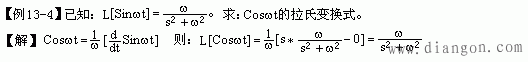
性质4°：时域积分性质。


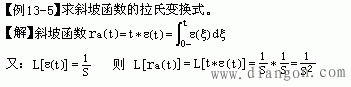
性质5°：时域平移性质（延迟性质或时滞定理）。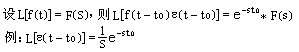

性质6°频域平移性质。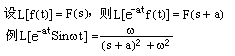

性质7°卷积定理。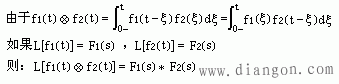

文章摘自电工电气学习网感谢分享